数据结构-排序算法摘要

分类与摘要

测试数据

int data[] = {13,7,2,5,1,58,15,27,44,10,31,8};

直接插入排序

直接插入排序流程案例：

//直接插入排序
 void InsertSort(int l[], int n){
     /*
     l: 源数据数组
     n: l的长度
     */
    for(int j,i=1;i<n;i++){
        if(l[i]<l[i-1]){
            int x = l[i];
            l[i] = l[i-1];
            for(j=i-2;j>=0&&x<l[j];j--){
                l[j+1] = l[j];
            }
            l[j+1] = x;
        }
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
    }
 }

时间复杂度为 O(N^2 )，空间复杂度为O(1)；

算法特点：

稳定排序；
算法简便，且容易实现；
同时适用于链式查找结构，且在查找过程中不需要移动记录，只需修改相应指针；
更适用于初始记录有序（正序）的情况，当初始记录无序，且 N 较大时，此算法的时间复杂度较高，不宜采用。

折半插入排序

折半插入排序流程案例：

//折半插入排序
 void BInsertSort(int l[],int n){
      /*
     l: 源数据数组
     n: l的长度
     */
    int x,low,high;
    for(int i=1;i<n;i++){
        x = l[i];
        low = 0;
        high = i-1;
        while(low <= high){
            int m = (low + high) / 2;
            if(l[m]>x)
                high = m-1;
            else
                low = m+1;
        }
        for(int j=i-1;j>=high+1;j--)
            l[j+1] = l[j];
        l[high+1] = x;
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
    }
 }

算法特点：

稳定排序；
只适用于顺序结构，不适用与链式结构；
适合初始记录无序，N 较大时情况。

希尔排序

根据增量对无序序列进行直接插入排序。

增量数组

int d[]={5,3,1}; //增量数组

//根据增量进行直接插入排序
 void ShellInsertSort(int *l,int d,int llen){
    /*
    l: 源数组
    d: 当前增量
    llen: l长度
    */
    for(int i=d;i<llen;i++){
        if(l[i]<l[i-d]){
            int k,x=l[i];
            for(k=i-d;k>=0&&x<l[k];k-=d){
                l[k+d] = l[k];
            }
            l[k+d] = x;
        }
    }
 }

 //希尔排序
 void ShellSort(int *l,int d[],int dlen,int llen){
    /*
    l: 源数据数组
    d: 增量数组
    dlen: 增量数组长度
    llen: 源数组长度
    */
    for(int i =0;i<dlen;i++){
        //根据增量每次进行直接插入排序
        ShellInsertSort(l,d[i],llen);
        //输出每次增量排序后的序列
        for(int k=0;k<llen;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
    }
 }

算法特点：

记录跳跃式的移动导致算法是不稳定的；
只能用于顺序结构，不能用于链式表；
增量序列可以有各种取法，但应该使增量序列中的值除了1之外没有其他公子，并且最后一个增量必须为1；
记录总的比较次数和移动次数比直接插入排序少，N 越大时，效果越明显。适用于初始记录无序，N 很大时的情况。

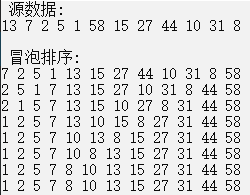
冒泡排序

冒泡排序是最简单的一种交换排序。

它通过比较相邻的交换记录，如果发现逆序，则进行交换，从而使得较小的记录不断往前“浮动”（左移），或者是较大的记录向下“坠落”（右移），从而达到排序的结果。

// 冒泡排序
 void BubbleSort(int *l, int n){
     int len = n;
     int flag = 1;
     while(len>0 && flag == 1){
        flag = 0;
        for(int i=0;i<len-1;i++){
            if(l[i]>l[i+1]){
                int x = l[i];l[i] = l[i+1];l[i+1] = x;
                flag =1;
            }
        }
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
        len --;
     }
 }

时间复杂度 O(N^2)，空间复杂度 O(1)

算法特点：

稳定排序；
可用于链式存储结构；
移动次数较多，算法平均时间性能比直接插入排序差。不适合初始记录无序，N 较大的情况。

快速排序

在待排序的记录 p[n] 中任取一个作为支点 pri，将记录表中小于pri的记录放在 pri 的左边，大于pri 的记录放在pri的右边，将记录表 p[n] 分为两个子表，然后对两个子表继续进行分表，将两个子表分为4个子表…..一直到记录表 p[n] 中的记录有序。

//获取中位
 int getFlag(int *l,int low,int high){
    int x = l[low];
    int flag = l[low];
    while(low<high){
        while(low<high && flag<= l[high]) --high;
        l[low] = l[high];
        while(low<high && flag>=l[low]) ++low;
        l[high] = l[low];
    }
    l[low] = x;
    return low;
 }

 //快速排序
 void FastSort(int *l,int low,int high){
     /*
     l: 原数组
     low: 低位
     high: 高位
     */
    if(low<high){
        int flag = getFlag(l,low,high);
        FastSort(l,low,flag-1);
        FastSort(l,flag+1,high);
    }
    // 每次排序遍历一次输出当前排序结果
    for(int k=0;k<12;k++){
        cout<<l[k]<< " ";
    }
    cout<<"\n";
 }

时间复杂度：O(nlog₂n)

空间复杂度：O(n)

算法特点：

记录非顺序的移动导致排序算法是不稳定的
适用于顺序结构，不适用于链式结构

简单选择排序

首先再所有记录中选出最小的记录，把它和第一个记录交换，然后在其余的记录中找出最小的记录，与第二个交换....直到所有记录排序完毕。

// 简单选择排序
 void SimpleSort(int *l,int n){
    for(int i=0;i<n;i++){
        int minx = i;
        for(int k=i;k<n;k++){
            if(l[minx]>=l[k]) minx=k;
        }
        if(minx!=i){
            int temp = l[i];
            l[i] = l[minx];
            l[minx] = temp;
        }
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
    }
 }

堆排序

堆排序详解：知乎-堆排序

// 堆排序的调整
void HeapAdjust(int *l,int start,int stop){
    int dads = start;
    int sons = dads * 2 + 1;
    while(sons<=stop){
        if(sons+1<=stop && l[sons]<l[sons+1])
            sons++;
        if(l[dads]>l[sons])
            return;
        else{
            {
                int x = l[dads];
                l[dads] = l[sons];
                l[sons] = x;
            }
            dads = sons;
            sons = dads*2 + 1;
        }
    }
}

// 堆排序
void HeapSort(int *l,int n){
    for(int i=n/2-1;i>=0;i--){
        HeapAdjust(l,i,n-1);
    }
    // 每次排序遍历一次输出当前排序结果
    for(int k=0;k<n;k++){
        cout<<l[k]<< " ";
    }
    cout<<"\n";
    for(int i=n-1;i>0;i--){
        {
            int x = l[i];
            l[i] = l[0];
            l[0] = x;
        }
        HeapAdjust(l,0,i-1);
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<l[k]<< " ";
        }
        cout<<"\n";
    }
}

并归排序

参考：维基百科-并归排序

void MergeAdjust(int *l,int *p,int low,int mid,int high){
    int i=low;
    int j=mid+1;
    int k = low;
    while(i<=mid && j<=high){
        if(l[i]<=l[j])
            p[k++] = l[i++];
        else
            p[k++] = l[j++];
    }
    while(i<=mid)   p[k++] = l[i++];
    while(j<=high)  p[k++] = l[j++];
    for(int i=low;i<=high;i++)
        l[i] = p[i];
}

void Merge(int *l,int *p,int low,int high){
    if(low == high)
        p[low] = l[low];
    else{
        int mid = (low+high)/2;
        Merge(l,p,low,mid);
        Merge(l,p,mid+1,high);
        MergeAdjust(l,p,low,mid,high);
    }
}

// 并归排序
void MergeSort(int *l,int n){
    int p[n];
    Merge(l,p,0,n-1);
    for(int k=0;k<n;k++){
        cout<<p[k]<< " ";
    }
    cout<<"\n";
}

基数排序

参考：菜鸟教程-基数排序

// 基数排序
void RadixSort(int *p,int n){
    int lens = MaxItem(p,n);
    int flags[n];
    int radix = 1;
    int k;
    int counts[10];
    for(int i=0;i<lens;i++){
        for(int j=0;j<10;j++)
            counts[j] = 0;
        for(int j=0;j<n;j++){
            k = (p[j]/radix) % 10;
            counts[k]++;
        }
        for(int j=1;j<10;j++)
            counts[j] = counts[j-1]+counts[j];
        for(int j=n-1;j>=0;j--){
            k = (p[j]/radix) % 10;
            flags[counts[k]-1] = p[j];
            counts[k]--;
        }
        for(int j=0;j<n;j++)
            p[j] = flags[j];
        radix *= 10;
        // 每次排序遍历一次输出当前排序结果
        for(int k=0;k<n;k++){
            cout<<p[k]<< " ";
        }
        cout<<"\n";
    }
}